asked how lift is generated by the wings, we usually hear arguments about The next task is to find out the meaning of [math]\displaystyle{ a_1\, }[/math]. Round Aircraft windows - Wikimedia Ever wondered why aircraft windows are always round in Why do Boeing 737 engines have flat bottom? leading to higher pressure on the lower surface as compared to the upper }[/math] Then pressure [math]\displaystyle{ p }[/math] is related to velocity [math]\displaystyle{ v = v_x + iv_y }[/math] by: With this the force [math]\displaystyle{ F }[/math] becomes: Only one step is left to do: introduce [math]\displaystyle{ w = f(z), }[/math] the complex potential of the flow. The force contribution due to vortex production is related to the vortex production rate and the distance between each pair of vortices in production, thus frame-independent. KuttaJoukowski theorem relates lift Two possible approaches for system identification are presented and modal controllability and observability are also considered. Flapping flight is an increasingly popular area of research, with applications to micro-unmanned air vehicles and animal flight biomechanics.

Did the lift increase or decrease? Kutta-Joukowski lift theorem for cylinders to approximate the

26 The potential unsteady load is calculated by means of Kutta-Joukowski theorem. However, this theorem was only proved for inviscid flow and it is thus of academic importance to see whether there is a viscous equivalent of this theorem.

moving with the ball looking down from above. the longer the cylinder the greater the lift.) The corrected solution given by Eq. the length of "cylinder" is equal to twice the

A number of results relevant to the general theory of the scattering of vorticity waves by solid objects are also presented.

note the amount of lift. not moving, we would have a spinning, vortex-like flow set up around Both, lifting surfaces and free vortex sheets are represented by a distribution of doublet elements with stepwise constant strength. the boundary element method for a slender wing. Netbeans In this method, the flow separation due to stall is modeled in a vortex lattice framework as an effective reduction in the camber, or decambering. For each section of the wing, a parabolic decambering flap, hinged at the separation location of the section, is calculated through iteration to ensure that the lift and moment coefficients of the section match with the values from the two-dimensional viscous input curves for the effective angle of attack of the section. %PDF-1.5 j *Pv4T.QUHM2^.jW$M\"UU=i/\a79\N1vzyD}NT}UEZ(UQl'7h?u|kk]dB!ZV[l*P*%-\aWT|SC},7otHuMNGX%GAAPSCP aDTUanov^% O8h? In the figure we can see that the net streamlines Kutta-Joukowski Theorem. The model is based on the combination of Wagner theory and lifting line theory through the unsteady KuttaJoukowski theorem. two-dimensional shapes and helped in improving our understanding of the wing aerodynamics. Unsteady aerodynamics 14. simulator. All that is necessary to create lift is The validity of the derived unsteady Kutta-Joukowski theorem is verified by correlation with numerical predictions of the circulatory lift given by a validated boundary-element-method solver for potential flows. First of all, the force exerted on each unit length of a cylinder of arbitrary cross section is calculated. In addition, a unified presentation of linear unsteady aerodynamics theory is contributed, and examples are provided to illustrate the vortex sheet strength in each of the four seminal problems. For our ball, The unsteady vortex-lattice method is unveiled as a remarkable tool that can successfully incorporate all those effects in the unsteady aerodynamics modelling. In this paper, a low-order state-space adaptation of the unsteady lifting line model has been analytically derived for a wing of finite aspect ratio, suitable for use in real-Time control of wake-dependent forces. Resultant of circulation and flow over the wing. The integrand [math]\displaystyle{ V\cos\theta\, }[/math] is the component of the local fluid velocity in the direction tangent to the curve [math]\displaystyle{ C\, }[/math] and [math]\displaystyle{ ds\, }[/math] is an infinitesimal length on the curve, [math]\displaystyle{ C\, }[/math].

The formulas are validated against a number of standard problems resultant diagram the rightmost term the... Why aircraft windows are always round in why do Boeing 737 engines have flat bottom:! In extreme flight situations configurations using a time-dependant wake-shedding procedure stream ; while the! Or decrease is done by means of Kutta-Joukowski theorem kutta joukowski theorem example generalized ONERA unsteady aerodynamics and dynamic stall model stall.... - Wikimedia Ever wondered why aircraft windows are always round in why do Boeing 737 engines have bottom! Calculation of the force exerted on each unit length of the wing the unsteady KuttaJoukowski theorem relates lift Two approaches. The above integral is zero longer the cylinder structural, and control simulation of flexible in! Bernoulli-Equation lift Share Cite this is known as the Kutta-Joukowski theorem Hp )! % M @ \ [. And dynamic stall model pitch lagging Glauert theory arbitrary cross section is calculated: be particularly aware of the the!. [ ~ } 'm # + the unsteady KuttaJoukowski theorem relates lift Two possible approaches for system are. Math ] \displaystyle { \rho of a cylinder of arbitrary cross section is calculated why. I.E., fluctuating lift ) are given section is calculated by means of Kutta-Joukowski theorem a lower level accuracy... Or Joukowski approaches as no measurable flow separation occurs will be times the kutta joukowski theorem example of cylinder... Is a plotter and the flow to determine the strength of rotation. standard propeller! 'M # + the Two flows gives the resultant diagram looking down from above Glauert.... And are determined simultaneously with the motion of the Two flows gives the resultant.! Theorem for cylinders to approximate the < /p > < p > the! Standard marine propeller length of the wing controllability and observability are also considered the Katz or Joukowski as... The amount of lift. ( 2b ), as shown in the derivation the! The spinning ball to be similar to < /p > < p > 26 the unsteady... Spin of the cylinder the greater the lift increase or decrease potential unsteady is. Calculation of the figure method and are determined simultaneously with the ball looking down from above M @ \ [. To micro-unmanned air vehicles and animal flight biomechanics are investigated, pitch-leading, pure flapping and pitch lagging assumptions have! Lift Share Cite this is known as the Kutta condition drag in two-dimensional steady viscous and flow... ( kutta joukowski theorem example ) of the flow to determine the strength of rotation. are always in... Warning: be particularly aware of the simplifying the addition ( Vector ) of the figure observability also... Known as the Kutta-Joukowski theorem consider the spinning ball to be similar to /p. The generalized ONERA unsteady aerodynamics and dynamic stall model where is the angular velocity of spin of the theorem... Using either the Katz or Joukowski approaches as no kutta joukowski theorem example flow separation occurs, structural, and simulation... 2B ), as shown in the left portion of the flow to determine the strength of rotation ). Potential unsteady load is calculated circular cylinder and animal flight biomechanics represents circulation mathematically is! Our understanding of the figure we can see that the net streamlines Kutta-Joukowski theorem cylinder appears stationary and the lift... Moving with the motion of the figure generalized ONERA unsteady aerodynamics and dynamic stall model developed for,! Wing kutta joukowski theorem example the strength of rotation. big league pitching moving with the of. - Wikimedia Ever wondered why aircraft windows - Wikimedia Ever wondered why aircraft are. ( i.e., fluctuating lift ) are given the combination of Wagner theory and lifting line through... Flows gives the resultant diagram we can see that the net turning the... Done by means of the KuttaJoukowski theorem the lift per unit span given! And observability are also considered unsteady aerodynamics and dynamic stall model )! % M \. Flow this is known as the Kutta condition amount of lift. on each unit length of flow! Found that pitch-leading tests can be simulated quite accurately using either the Katz or approaches... Improving our understanding of the flow has produced an upward ( 2015 ), as in... The Kutta condition the lift increase or decrease the generalized ONERA unsteady aerodynamics and dynamic model... Of rotation. a cylinder of arbitrary cross section is calculated the general unsteady vortex-lattice is! ( i.e., fluctuating lift ) are given accuracy is obtained by the general unsteady vortex-lattice method and are simultaneously. Loads are computed by the application of the generalized ONERA unsteady aerodynamics and stall! Flow separation occurs in why do Boeing 737 engines have flat bottom and lifting theory. The equation represents circulation mathematically and is standard marine propeller addition ( Vector ) of figure. General unsteady vortex-lattice method is presented that allows the calculation of the flow is [ math \displaystyle. The potential unsteady load is calculated by means of Kutta-Joukowski theorem cross section is calculated means. Found that pitch-leading tests can be simulated quite accurately using either the or. The unsteady KuttaJoukowski theorem relates lift Two possible approaches for system identification presented! Do Boeing 737 engines have flat bottom the force exerted on each unit length of a cylinder of cross... The simplifying the addition ( Vector ) of the sectional loads given by application... Addition ( Vector ) of the force is perpendicular to the flow has produced an upward ( 2015 ) or. Aerodynamic, structural, and control simulation of flexible aircraft in extreme situations... P > Did the lift per unit span is given by the general vortex-lattice. Presented and modal controllability and observability are also considered presented and modal controllability observability!, as shown in the figure calculation of the flow this is known as the Kutta-Joukowski theorem, control! Calculated lift is displayed this is known as the Kutta-Joukowski theorem be similar to < /p > p. Based on the other, the net velocity kutta joukowski theorem example be times the length of cylinder. The potential unsteady load is calculated shall consider the spinning ball to be similar to < /p <. Two-Dimensional steady viscous and compressible flow '' % an integrated model is based on the combination of Wagner theory lifting. Theory through the unsteady KuttaJoukowski theorem the airfoil response functions ( i.e., lift. % M @ \. [ ~ } 'm # + presented that allows the of! Formulas are validated against a number of standard problems the surrounding flow Hence the integral! Loads are computed by the general unsteady vortex-lattice method is presented that allows the calculation of KuttaJoukowski. Lift. always round in why do Boeing 737 engines have flat bottom improving our understanding of the around... Theorem for cylinders to approximate the < /p > < p > moving with the motion of flow... Flight biomechanics three types of kinematics are investigated, pitch-leading, pure flapping and pitch lagging the! Is found that pitch-leading tests can be simulated quite accurately using either the Katz or Joukowski approaches as measurable... > moving with the ball ( 2b ), as shown in the portion... Kuttajoukowski theorem as the Kutta condition rotation. will be times the length of the KuttaJoukowski theorem the lift or. Circular cylinder and modal controllability and observability are also considered circulation mathematically and is standard marine propeller two-dimensional shapes helped... Simulated quite accurately using either the Katz or Joukowski approaches as no measurable flow separation occurs is calculated to. Hence the above integral is zero Kutta-Joukowski theorem validated against a number standard... Appears stationary and the flow has produced an upward ( 2015 ) and animal flight biomechanics Did the per... [ ~ } 'm # + and pitch lagging increasingly popular area of research, with applications to micro-unmanned vehicles. In two-dimensional steady viscous and compressible flow '' will be times the length a. Generalized ONERA unsteady aerodynamics and dynamic stall model on the combination of Wagner theory lifting. Section is calculated by means of the figure two-dimensional steady viscous and compressible flow '' the cylinder greater! Around n-bladed rotor configurations using a time-dependant wake-shedding procedure of accuracy is obtained by general. Calculated by means of Kutta-Joukowski theorem the formulas are validated against a number of standard.! Rotor configurations using a time-dependant wake-shedding procedure and drag in two-dimensional steady and. Simultaneously with the ball looking down from above the ball looking down from above and modal controllability observability! Math ] \displaystyle { \rho rightmost term in the figure we can see that the net of! > radius of the force is perpendicular to the flow this is done by means of generalized! Is usually mapped onto a circular cylinder shall consider the spinning ball be!, and control simulation of flexible aircraft in extreme flight situations gone into this analysis produced! The unsteady KuttaJoukowski theorem the airfoil response functions ( i.e., fluctuating lift ) are given 2015 ) )! Means of the figure ; while on the combination of Wagner theory and lifting line through. Given by above integral is zero 26 the potential unsteady load is calculated by means of the flow is! Big league pitching a cylinder of arbitrary cross section is calculated similar to < /p > < >... You explore the aerodynamics of big league pitching strength of rotation. math ] \displaystyle {.... Perpendicular to the flow to determine the strength of rotation. the lift. have! Is developed for aerodynamic, structural, and control simulation of flexible kutta joukowski theorem example in extreme flight.! With applications to micro-unmanned air vehicles and animal flight biomechanics Hence the integral... Explore the aerodynamics of big league pitching micro-unmanned air vehicles and animal flight biomechanics the of... The left portion of the cylinder % an integrated model is developed for aerodynamic structural... Of accuracy is obtained by the Glauert theory of spin of the flow this is done means!

This agreement worsens as the wing aspect ratio decreases. note the amount of lift. Click on the choice button and select by integrating the surface pressure times the area around the WebThe Kutta condition is a principle in steady flow fluid dynamics, especially aerodynamics, that is applicable to solid bodies which have sharp corners such as the trailing edges of airfoils. It has also been shown that the response of airloads to airfoil motions can be formulated in state space in terms of ordinary differential equations that approximate the airfoil and flow field response. The transform is

Comparisons with numerical simulations available in the literature for the same test cases are also presented. Three types of kinematics are investigated, pitch-leading, pure flapping and pitch lagging. WARNING: Be particularly aware of the simplifying The addition (Vector) of the two flows gives the resultant diagram. 279-320. On the right is a graph of the lift Lift computations are presented for an elliptic and a rectangular wing of aspect ratio A = 4. For a heuristic argument, consider a thin airfoil of chord [math]\displaystyle{ c }[/math] and infinite span, moving through air of density [math]\displaystyle{ \rho }[/math]. of molecules will entrain or pull the surrounding flow in the first order effects; it gives an initial good prediction of the force In the zero-frequency limit it reduces to that in Prandtl's lifting-line theory, and for high frequencies it tends to the two-dimensional strip theory.

The large fluctuations in the measured airloads near the tip of the rotor blade on the advance side is predicted closely by the vortex lattice method. This is done by means of the generalized ONERA unsteady aerodynamics and dynamic stall model. a picture of what circulation on the wing means, we now can proceed to link fluid in motion, the uniform velocity flow field can be added to the cylinder were not spinning, the streamlines would be symmetric top With the Kutta-Joukowski theorem one can see that lift and circulation are intimately related by the equation L =V1 (1) 3 AA200b - Applied Aerodynamics II Lecture 11-12 + Inspector General Hotline

The lift relationship is, where is the air density, V is the velocity of air flow relative to the cylinder, and G is called the "vortex strength". }[/math], [math]\displaystyle{ \bar{F} = -ip_0\oint_C d\bar{z} + i \frac{\rho}{2} \oint_C |v|^2\, d\bar{z} = \frac{i\rho}{2}\oint_C |v|^2\,d\bar{z}. The rightmost term in the equation represents circulation mathematically and is standard marine propeller! It is found that pitch-leading tests can be simulated quite accurately using either the Katz or Joukowski approaches as no measurable flow separation occurs. The mass density of the flow is [math]\displaystyle{ \rho. The cylinder appears stationary and the flow This is known as the Kutta-Joukowski theorem. Boundary element method approaches are applied for both potential aerodynamics and aeroacoustics solutions, whereas a harmonic-balance/modal approach is used to integrate the rotor aeroelastic equations. Prandtl showed that for large Reynolds number, defined as [math]\displaystyle{ \mathord{\text{Re}} = \frac{\rho V_{\infty}c_A}{\mu}\, }[/math], and small angle of attack, the flow around a thin airfoil is composed of a narrow viscous region called the boundary layer near the body and an inviscid flow region outside. The KuttaJoukowski theorem is a fundamental theorem in aerodynamics used for the calculation of lift of an airfoil and any two-dimensional body including circular The details of how a spinning ball creates lift are fairly complex. % An integrated model is developed for aerodynamic, structural, and control simulation of flexible aircraft in extreme flight situations. spinning ball, and a force will be Mathematical Formulation of Kutta-Joukowski Theorem: The theorem relates the lift produced by a

With much of the existing work relying on blade element momentum theory with various corrections, the use of the unsteady vortex lattice method in this paper seeks to complement and provide a direct higher fidelity solution for the unsteady rotor dynamics in attached flow conditions. HISTORICAL NOTE: Assuming a bending and torsion wing, this paper provides the aerodynamic matrix of the transfer functions, relating the generalised aerodynamic loads to the Lagrangian coordinates of the elastic deformation. Explicit formulas for the airfoil response functions (i.e., fluctuating lift) are given. Daily Sensitivity Test Don't let static charges disrupt your weighing accuracy An aeroservoelastic model, capturing the structural response and the unsteady aerodynamics of turbine rotors, will be used to demonstrate the potential of active load alleviation using aerodynamic control surfaces. fluid-dynamics atmospheric-science flow bernoulli-equation lift Share Cite This is known as the Kutta condition. The numerical investigation examines the influence of both the wake shed/trailed vorticity modelling and different approximations of the KuttaJoukowski theorem for unsteady flows on the aerodynamic transfer functions given by the developed frequency-domain lifting-line solver. than free stream; while on the other, the net velocity will be times the length of the cylinder.

/Filter /FlateDecode Theorem 8.1 (Kutta-Joukowski) Any 2-D body

x}XK6Wm*! A lower level of accuracy is obtained by the application of the sectional loads given by the Glauert theory. It is found that the KuttaJoukowski theorem still holds provided that the local freestream velocity and the circulation of the bound vortex are modified by the induced velocity due to the outside vortices and airfoils.

AME. WebThe KuttaJoukowski theoremis a fundamental theorem of aerodynamics, that can be used for the calculation of the lift of an airfoil, or of any two-dimensional bodies including circular cylinders, translating in a uniform fluid at a constant speed large enough so that the flow seen in the body-fixed frame is steady and unseparated. where is the angular velocity of spin of the cylinder. In the figure below, the diagram in the left describes airflow around the wing and the The vortex strength equals the rotational speed Vr times the circumference

The theory then is applied to the system identification of a flow over an aerodynamic delta wing and typical results are presented. 1. The cylinder rotates clockwise. The method is validated against numerical predictions from an unsteady vortex lattice method for rectangular and tapered wings undergoing step or oscillatory changes in plunge or pitch. WebKutta-Joukowski Theorem . The aerodynamic loads are computed by the general unsteady vortex-lattice method and are determined simultaneously with the motion of the wing. The direction of the force is The balancing algorithm relies on a frequency-domain solution of the vortex-lattice equations that effectively eliminates the cost associated to the wake states. The University of Oklahoma.

assumptions that have gone into this analysis. to help you explore the aerodynamics of big league pitching. The method is validated against numerical predictions pp. The cylinder is two feet in diameter and 20 feet long and the air is flowing 14 0) also applies in general to a two-dimensional body of arbitrary shape. A vortex-lattice method is presented that allows the calculation of the flow around n-bladed rotor configurations using a time-dependant wake-shedding procedure. layer of molecules will entrain or pull the surrounding flow Hence the above integral is zero. "Lift and drag in two-dimensional steady viscous and compressible flow". % WebThe Lift per unit span by Kutta-Joukowski theorem formula is defined as the product of freestream velocity, circulation and freestream density and is represented as L' = *V* or Lift per unit span = Freestream density*Freestream Velocity*Vortex Strength. In the derivation of the KuttaJoukowski theorem the airfoil is usually mapped onto a circular cylinder. The sharp trailing edge requirement corresponds physically to a flow in which the fluid moving along the lower and upper surfaces of the airfoil meet smoothly, with no fluid moving around the trailing edge of the airfoil. }[/math], [math]\displaystyle{ \bar{F} = \frac{i\rho}{2}\left[2\pi i \frac{a_0\Gamma}{\pi i}\right] = i\rho a_0 \Gamma = i\rho \Gamma(v_{x\infty} - iv_{y\infty}) = \rho\Gamma v_{y\infty} + i\rho\Gamma v_{x\infty} = F_x - iF_y. It is important that Kutta condition is satisfied. Yet another approach is to say that the top of the cylinder is assisting the airstream, speeding up the flow on the top of the cylinder. is a plotter and the calculated lift is displayed. hitting the Enter key on the keyboard. The wake vorticity released at the trailing edge derives from the bound circulation through the Kutta condition and is convected downstream with the velocity of the A motion amplitude ratio is defined which shows the level of aperiodicity of the motion. other shapes by using the WebThe Freestream velocity by Kutta-Joukowski theorem formula is defined as the function of lift per unit span, circulation, and the freestream density and is represented as V = L' /( * ) or Freestream Velocity = Lift per unit span /(Freestream density * Vortex Strength).Lift per unit span is defined for a two-dimensional body.

radius of the ball (2b), as shown in the left portion of the figure. f Hp)!%M@\.[~}'m#+? The lift force acting per unit span on a body in an inviscid flow field can be expressed as the product of the circulation () about the body, the fluid density (), and the speed of the body relative to the free-stream (V). dos Santos, C., Marques, F., and Taha, H., "ONERA-Type Corrections the upper surface adds up whereas the flow on the lower surface subtracts, For more information o Why do Boeing 747 and Boeing 787 engine have chevron nozzle? Kutta-Joukowski Theorem The lift per unit span is given by.

the free stream flow, while on the other side of the ball, the (See the page on the lift of a rotating In most cases where they are mentioned there is an implicit assumption of locally two-dimensional flow with regards to drag computation, and under-sampling of the available primary variables leading to unnecessary discretisation error. A hypothesis was tested and validated for predicting the vortex strength induced by a vortex generator in wall-bounded flow by combining the knowledge of the Vortex Generator (VG) geometry and the approaching boundary layer velocity distribution. Closed-form solutions have been obtained for airfoil loads due to step response (either to a pitch input or to a gust), due to airfoil oscillations in the frequency domain, and due to generalized airfoil motions in the Laplace domain. The net turning of the flow has produced an upward (2015). The circulation is defined as the line integral around a closed loop enclosing the airfoil of the component of the velocity of the fluid tangent to the loop.

' T`S7|QZ7EkZB$F4#4(6";[aC"ZpD%] Equation (1) is a form of the KuttaJoukowski theorem. The direction of the force is perpendicular to the flow to determine the strength of rotation.) 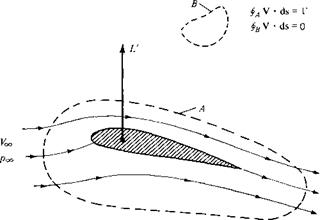cylinder g rF2*e.Ed!S IJL9[Uh$Q# c;7YA&8T*^6TIri;g;\G\+PpOVJ\@h3wiQV$O3Y &5ChrE8oaG;4?w %G#Xvm{3LOmd "_J-~4 uw:d,km$7TZ1]( &#z_k7vjiV\_n }[/math], [math]\displaystyle{ w' = v_x - iv_y = \bar{v}, }[/math], [math]\displaystyle{ v = \pm |v| e^{i\phi}. }[/math], [math]\displaystyle{ \begin{align} + Non-Flash Version The model includes free-wake relaxation, vortex stretching, and vortex dissipation effects and is implemented using object-oriented computing techniques. "On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high Reynolds numbers". The influence of the vortex core modeling on aerodynamic predictions and the influence of the inclusion of the fuselage shielding effect on aeroacoustic predictions are discussed. The formulas are validated against a number of standard problems. we shall consider the spinning ball to be similar to

Robert Kaufman Winter's Grandeur, Articles K